Решение системной задачи поиска эффективных способов обеспечения надежности и качества зубчатых передач предлагается на основе автоматизации проектирования и параметрического синтеза многопарного зацепления.

Зубчатые передачи (ЗП) как часть привода технологических агрегатов в значительной мере определяют их основные технико-экономические показатели: массу, габариты, ресурс, уровень шума и вибраций, стоимость и т. д. Для зубчатых передач требования к их надежности и качеству во многом противоречивы. В этих условиях осуществляется поиск компромиссных вариантов на основе оптимизации параметров передач по заданным критериям качества.
Реализация данной задачи возможна как традиционными средствами, так и за счет новых технических решений. Традиционные способы — путем повышения точности изготовления и сопротивляемости передач действующим нагрузкам, например, за счет увеличения размеров, применения высокопрочных материалов и т. д., требуют значительных материальных затрат и не всегда приводят к желаемым результатам. Одним из методов снижения затрат и оптимизации показателей качества передач является автоматизация процесса их проектирования на основе программно-методических комплексов (ПМК). В общем случае ПМК представляет собой иерархическую блочную структуру в виде пакета прикладных компьютерных программ по расчету геометрии и прочности передач. ПМК имеет модульное построение и организован как единая технологическая система для получения, модификации и передачи данных на всех этапах параметрического расчета. Содержание ПМК составляют методики, алгоритмы и программы для автоматизации расчета и проектирования передач. Методическое обеспечение ПМК основывается на использовании как стандартных, так и оригинальных методик. Типовая структура математического и программного обеспечения (МО и ПО) ПМК приведена на рис. 1.

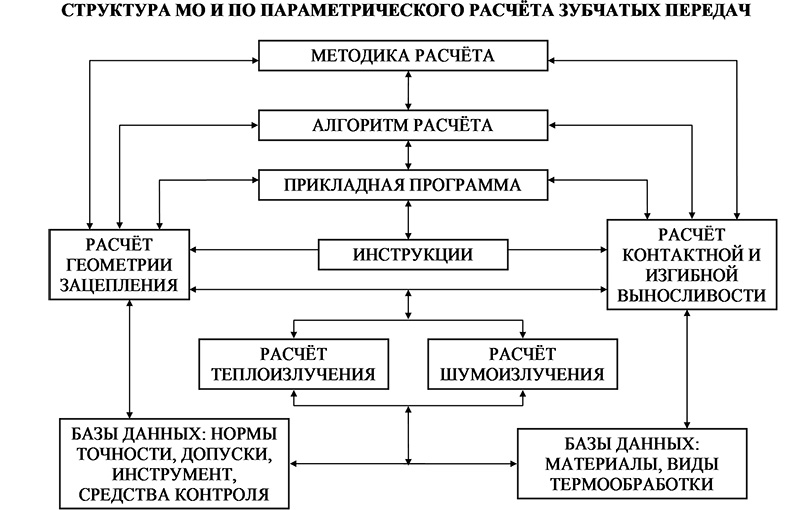
Рис. 1. Структура ПМК для зубчатых передач

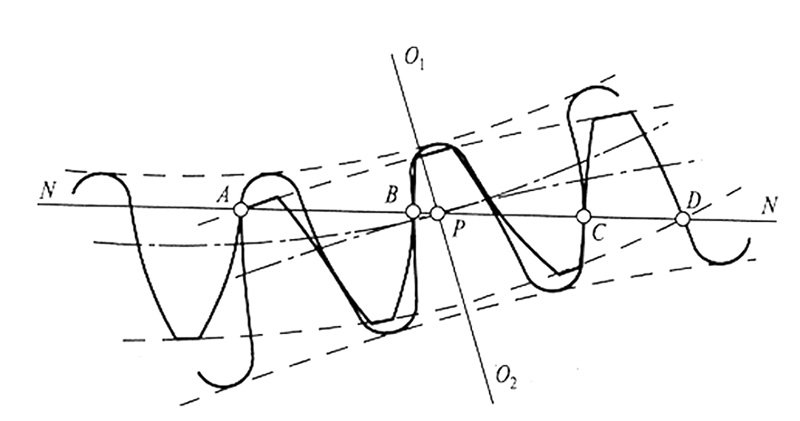
Рис. 2. Схема двухпарного зацепления

Как следует из рис. 1, связи между блоками ПМК организованы по принципу обратной связи, что позволяет оперативно модифицировать содержание ПМК. Все компьютерные программы выполнены в виде исполняемых модулей типа «exe» и могут работать в пакетном и диалоговом режимах с операционными системами Windows и Vista. МО и ПО данного ПМК позволяют моделировать передачи на основе как традиционных, так и инновационных технологий. К новым техническим решениям, обеспечивающим более высокий уровень качества ЗП, можно отнести проектирование передач с многопарным зацеплением. Такие передачи за счет одновременного контакта нескольких пар зубьев имеют более высокие показатели по прочности, ресурсу и шуму по сравнению с передачами с однопарным зацеплением. Показателем многопарного зацепления (рис. 2) является коэффициент торцового перекрытия ε_α, характеризующий отношение длины активной линии зацепления AD к шагу зацепления AB, численное значение которого должно быть больше двух. Синтез передач с многопарным контактом производится путем оптимизации геометрии зацепления по критерию ε_α > 2 и при условии обеспечения максимальной прочности передач при минимальных габаритах. Функция оптимизации, например, для цилиндрических передач внешнего зацепления при граничных условиях по подрезанию, интерференции и заострению зубьев имеет при этом вид:
              ε_α = F (z_c, x_c, α, h*_a, β ) > 2,                             (1)
где, z_c, x_c — суммарные значения чисел зубьев и коэффициентов смещений зубчатых пар; α, h*_a, β — угол профиля, коэффициент высоты головки исходного контура и угол наклона зубьев.
Величина коэффициента ε_а не зависит от модуля передачи m. Это позволяет осуществлять геометрический синтез многопарного зацепления при значениях m = 1, а также оптимизировать габариты передачи путем увеличения значений m. Так как контактные и изгибные напряжения на зубьях зависят от величины модуля, то увеличение модуля допустимо до значений, при которых расчетные контактные и изгибные напряжения должны быть меньше или равны допускаемым. Значения последних выбираются в зависимости от свойств материала зубчатых пар, режимов термообработки, заданного ресурса и т. д. В результате задача синтеза многопарной передачи сводится к параметрическому синтезу передачи по критерию (1) и условиям прочностной выносливости при минимальных габаритах.
Оптимальный синтез передач по указанным условиям возможен в основном только с помощью специальных компьютерных программ. Пакетный режим ПМК используется для получения значений параметров в первом приближении. Диалоговый режим позволяет оптимизировать параметры передач в соответствии с заданными ограничениями. Синтез геометрии многопарного зацепления производится путем высотно-профильной модификации зубьев при значениях параметров исходного контура α ≤ 20° и h*_a >1. В табл. 1–4 представлены основные параметры геометрии цилиндрических ЗП внешнего зацепления с 2‑х, 3‑х, 4‑х и пятипарным зацеплением [1, 2, 3, 4] при условии, что m = 1 и отсутствуют подрез, заострение и интерференция зубьев.

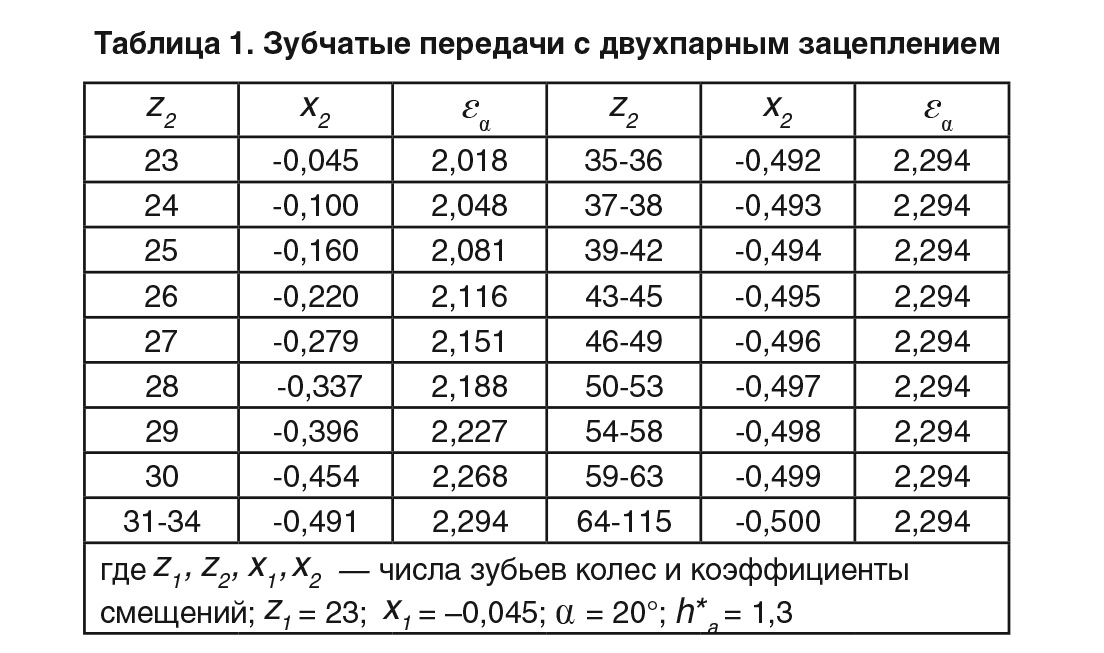
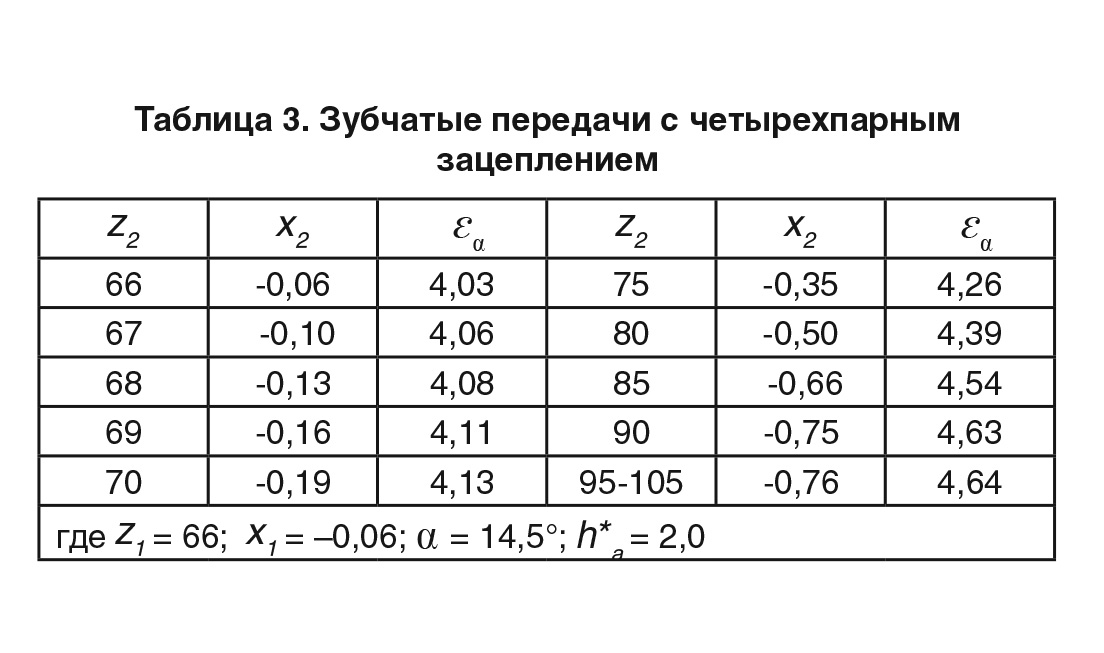
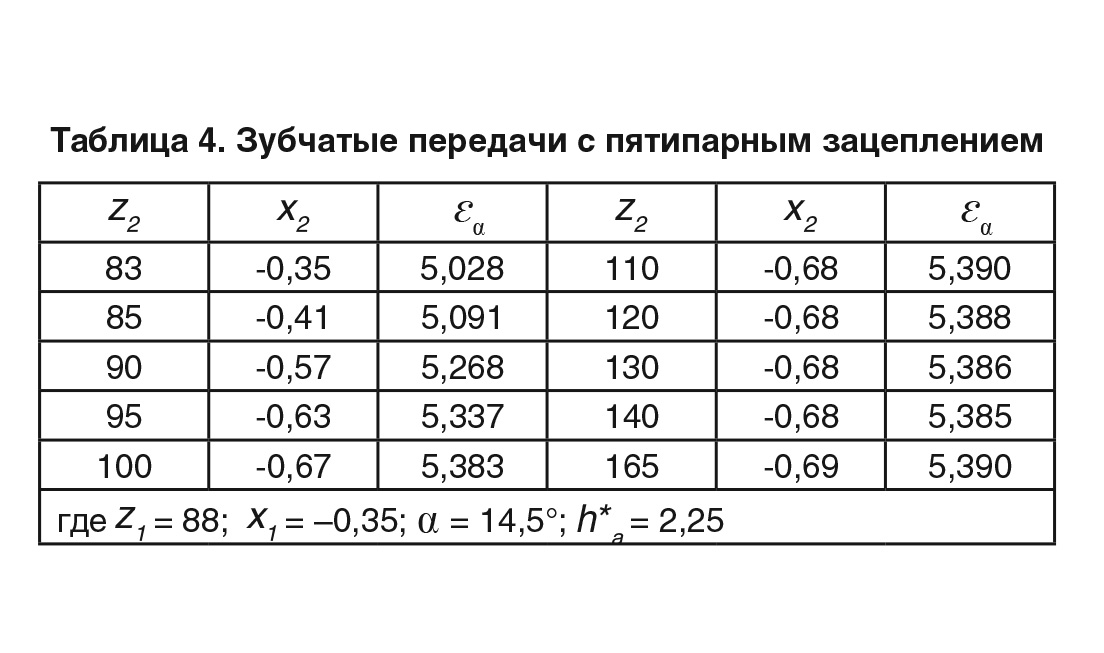
Как видно из таблиц, многопарное зацепление осуществляется при разных значениях параметров исходного контура. Выбор параметров производится на основе анализа значений потенциально возможного коэффициента торцового перекрытия ε_α0 [5]:
               ε_α0 =  4 . h*_a /  п sin 2α  .                                   (2)
Для стандартного исходного контура ε_α0 = 1,98, т. е. многопарное зацепление со стандартными параметрами исходного контура теоретически неосуществимо. С уменьшением угла а профиля и увеличением коэффициента высоты головки h*_a значение коэффициента ε_α увеличивается.
В общем случае величина парности зацепления может быть увеличена до любого наперед заданного значения N, где N — целая часть величины коэффициента ε_α. В таблице 5, например, приведены значения параметров геометрии ЗП с 10‑парным зацеплением.

Анализ таблиц 1–5 показывает, что возможности синтеза передач с любым n-парным зацеплением теоретически не ограничиваются при условии, что удовлетворяются основные требования существования зацепления:
                       m > 0, z₁ > 3, z₂ > 3   
                       0 < α_tw < 90°              ,                          (3)
                       d_b < d_a
где α_tw — угол зацепления; d_b — диаметр основной окружности зубчатых колес; d_a — диаметр внешней окружности зубчатых колес.
Автоматизация геометрического синтеза ЗП на основе ПМК позволяет проектировать передачи в соответствии с условиями (1–3) с любой наперед заданной величиной коэффициента ε_α. Для обоснованного выбора параметров геометрии многопарных передач кроме собственно геометрического синтеза зацепления требуется также силовой и прочностной анализ передач. В первом приближении без учета жесткости и погрешностей изготовления передач сила давления на зубья в зоне контакта определяется выражением:
                    F_Y =   M_K / ( n . R_Y . cos α_Y . cos β_b) ,                    (4)
где M_K — крутящий момент на зубчатом колесе, H.м; n — число пар одновременно контактирующих зубьев; R_Y  — радиус-вектор в точках контакта зубьев, м; α_Y — угол давления в точках контакта, градус; β_b — основной угол наклона, градус.
Выражение (4), непосредственно характеризующее зависимость нагрузки на зубья от величины парности зацепления, можно использовать и для оценки прочностной выносливости передач. По аналогии с (4) и с учетом ГОСТ на расчет прочности ЗП [6] расчетные напряжения в полюсе зацепления зубчатого колеса многопарной передачи будут определяться выражениями:
             σ_H = K_Z . √( K_H . F_t . (и + 1)) / (n . b_w . d_w . и)  ;      (5)
                                    
             σ_F = K_F . K_Y .  ( F_t / ( n . b_w . m)) ,     (6)
                                
где σ_H, σ_F — соответственно расчетные контактные и изгибные напряжения на зубьях, МПа; K_H, K_F — коэффициенты нагрузки соответственно при контакте и изгибе; F_t — суммарная окружная сила на начальном цилиндре в торцовом сечении, Н; K_Z — коэффициент, учитывающий механические свойства материалов зубчатых колес, форму сопряженных поверхностей зубьев, суммарную длину контактных линий и угол наклона зубьев при контактном нагружении; K_Y — коэффициент, учитывающий влияние формы зуба и концентрации напряжений; b_w, d_w — соответственно ширина зубчатого венца и начальный диаметр шестерни, мм; и — передаточное число.
Согласно теории зацеплений, активная линия зацепления пары зубьев состоит их двух участков — зон однопарного и двухпарного зацепления. Целая часть коэффициента ε_α, т. е. INT (ε_α) = n, а дробная часть (мантисса) характеризует область (n + 1)-парного зацепления. При этом в многопарном зацеплении передаваемая нагрузка распределяется между контактирующими парами зубьев неравномерно, что можно учитывать дополнительно соответствующим коэффициентом неравномерности
Kn = 1,1–1,25 в зависимости от величины n, жесткости контакта, точности передачи и т. д. В соответствии с этим формулы (5)—(6) принимают вид:
             σ_H = K_Z . √ K_H . K_n . ( F_t . (и + 1)) /(ε_α . b_w . d_w . и ) )     ;  (7)
                                        
            σ_F = K_F . K_Y . K_n .  ( F_t / ( ε_α . b_w . m)) . (8)
                                     
В качестве примера в таблице 6 приведены результаты геометрического и прочностного расчета ЗП механизма газораспределения дизельного агрегата с одно- и многопарным зацеплением при сохранении габаритов передачи с использованием зависимостей (7) — (8).

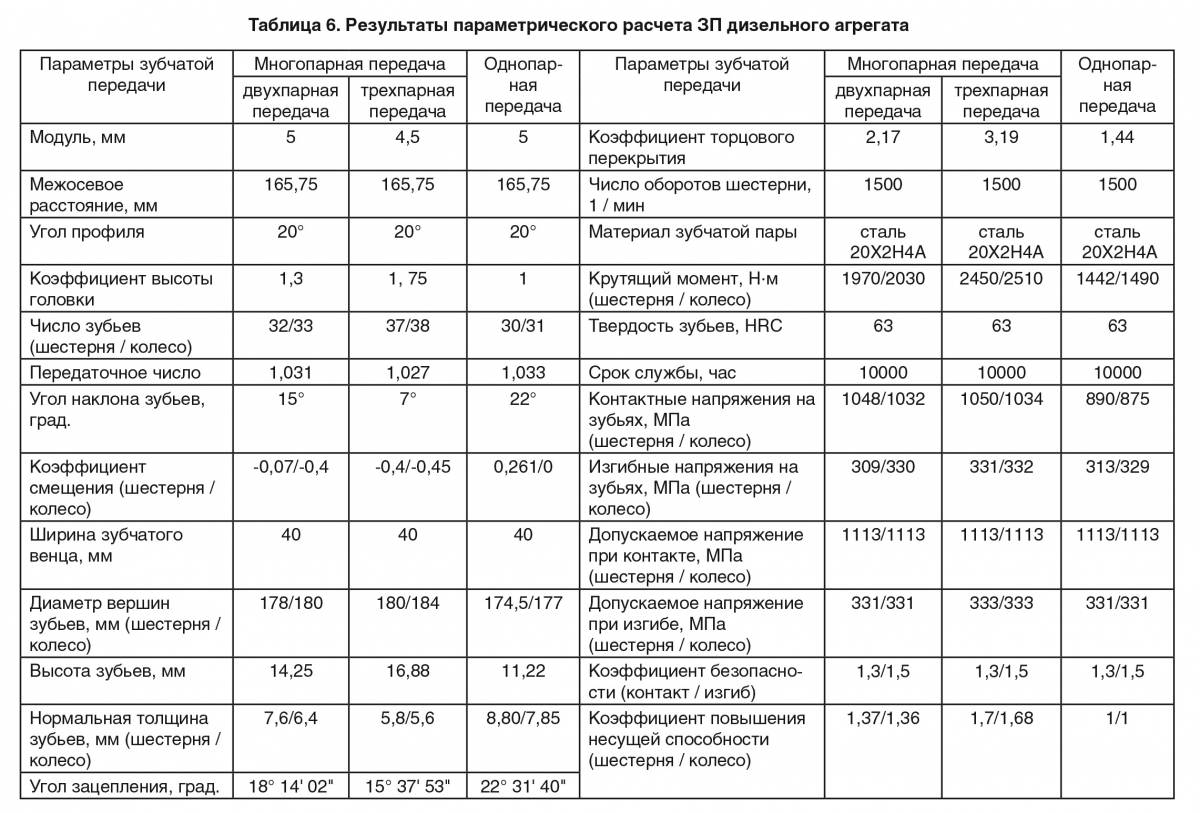
Как следует из таблицы 6, передачи с двух- и трех-парным зацеплением могут передавать значительно больший крутящий момент — соответственно в 1,4 и 1,7 раза по сравнению с однопарной передачей при одинаковых габаритных размерах. В реальных передачах, как показали результаты испытаний многопарных передач на ОАО «ГАЗ» и ОАО «Автодизель», указанный эффект может быть даже несколько больше, что в определенной степени объясняется относительным несовершенством методик прочностного расчета ЗП. Так как основное преимущество передач с многопарным зацеплением — это снижение нагрузки на зубья при n-парном контакте, то на основе условий (1) — (8) можно проектировать передачи с большим передаваемым моментом и ресурсом при уменьшенных габаритах. Повышение ресурса и несущей способности передач достигается путем увеличения парности зацепления, а уменьшение габаритов — за счет уменьшения модуля. На основе допустимого компромисса между этими направлениями можно одновременно как повышать несущую способность и надежность передач, так и минимизировать их размеры. Реализация данных решений возможна в основном только с применением ПМК по расчету ЗП.

Литература
1. Таратынов О. В., Клепиков В. В., Мельников В. З. Цилиндрическая зубчатая передача внешнего зацепления с двухпарным зацеплением зубьев. Патент РФ на полезную модель № 101759. Бюл. № 3 от 27.01.2011.
2. Таратынов О. В., Клепиков В. В., Мельников В. З. Цилиндрическая зубчатая передача внешнего зацепления с трехпарным зацеплением зубьев. Патент РФ на полезную модель № 115848. Бюл. № 13 от 10.05.2012.
3. Таратынов О. В., Мельников В. З., Клепиков В. В. Цилиндрическая зубчатая передача внешнего зацепления с четырехпарным зацеплением зубьев. Патент РФ на полезную модель № 121330. Бюл. № 29 от 20.10.2012.
4. Таратынов О. В., Мельников В. З., Клепиков В. В. Цилиндрическая зубчатая передача внешнего зацепления с пятипарным зацеплением зубьев. Патент РФ на полезную модель № 121329. Бюл. № 29 от 20.10.2012.
5. Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач. Под ред. И. А. Болотовского. М.: Машиностроение, 1986. 447 с.
6. ГОСТ 21354–87 «Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность».