Конические передачи (с прямыми и криволинейными зубьями) относятся к числу безальтернативных зубчатых передач и широко используются в трансмиссиях привода различных технологических и транспортных агрегатов. Обеспечение эффективности их применения, в частности, за счет повышения несущей способности и ресурса представляет собой сложную научно-техническую задачу.
Традиционные способы решения — путем повышения сопротивляемости передач действующим нагрузкам и точности их изготовления являются существенно затратными и не всегда результативными. Альтернативный путь решения — это снижение контактных давлений на зубья за счет одновременного взаимодействия нескольких пар зубьев, т. е. на основе многопарного зацепления. Обеспечение многопарного контакта в передаче возможно при условии, если активная линия зацепления будет больше двух шагов зацепления и коэффициент перекрытия εα, численно будет больше двух, т. е. должно выполняться условие:
εα > 2. (1)
Реализация условия (1) производится путем модификации исходных данных на основе компьютерного моделирования геометрии передачи. Как показывает анализ выражений, определяющих геометрию конических передач [1], [2], величина коэффициента εα зависит в основном от значений параметров исходного контура, чисел зубьев и коэффициентов смещений, т. е.
εα = F(zc, xc, α, hα*, β ) > 2, (2)
где zc, xc — суммарные значения чисел зубьев и коэффициентов смещений зубчатых пар; α, hα*, β — угол профиля и коэффициент высоты головки исходного контура и угол наклона зубьев.
Геометрия многопарной передачи определяется путем высотно-профильной модификации исходного контура в пределах: α ≤ 20°; hα* >1, а также возможных смещений производящего контура. В n- парной передаче, где n- целая часть коэффициента перекрытия εα, величина парности зацепления n определяется как функция от значения εα, т. е.
n = INT (εα), (3)
где INT — оператор функции наибольшего целого числа, не превосходящего заданное числовое значение.
В общем случае активная линия зацепления состоит их двух участков — зон n- парного и (n + 1) — парного зацепления. При этом целая часть коэффициента εα, т. е. INT(εα) = n, а дробная часть характеризует область (n+1)-парного зацепления. Предварительный расчет передач по условию (1) производится на основе анализа потенциально возможных значений коэффициента перекрытия εα0:
εα0 = (4 . hα*)/(п . sin2α). (4)

Значения коэффициентов для отдельных исходных контуров приведены в таблице 1. Как следует из таблицы 1 условие (1) для передач со стандартным исходным контуром теоретически не осуществимо. Для реализации условия (1) необходима модификация как исходного, так и соответственно производящего контура. В общем случае для изготовления — парных передач требуется зуборезный инструмент, соответствующий выбранному исходному контуру.
В отдельных случаях при изготовлении передач только с высотной модификацией зубьев, когда α = 20°, а hα*>1, можно использовать и стандартный инструмент, так как коэффициент высоты профиля инструмента h0* ≥ 2,4÷2,5.
В частности, за счет уменьшения радиального зазора в передаче до 0.05÷0,1 модуля m в допустимых пределах можно увеличивать высоту профиля зубьев и обеспечивать условие (1).

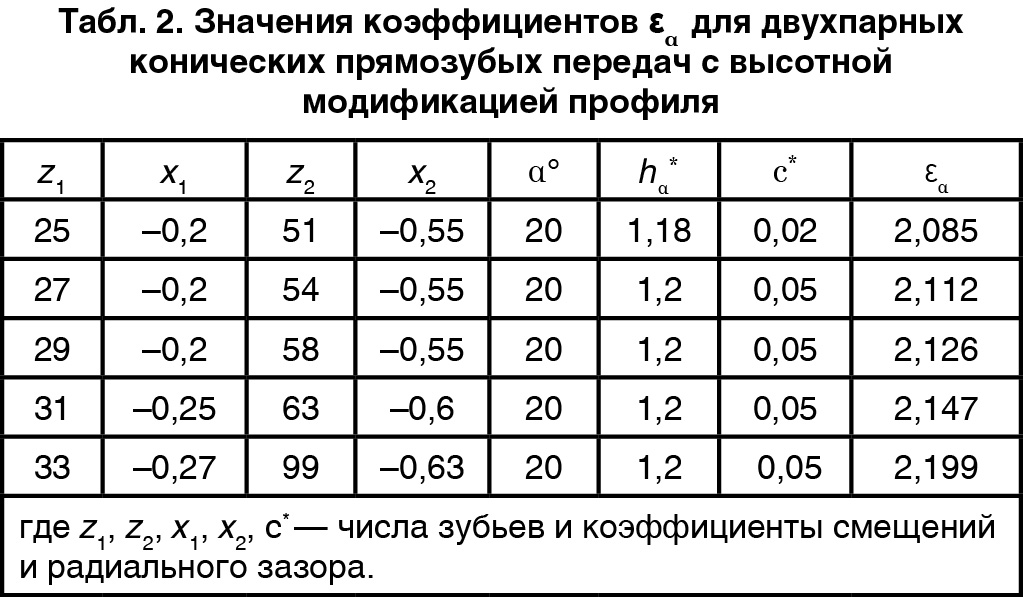
В таблице 2, например, приведены значения коэффициентов εα для двухпарных конических прямозубых передач с высотной модификацией профиля и исходными данными, исключающими подрез, интерференцию и заострение зубьев. Расчет передач производится при значениях m = 1, так как величина коэффициента εα в общем случае от модуля не зависит.

Как видно из таблицы 2 при высотной модификации исходного контура и использовании стандартного инструмента полная высота зубьев может быть  увеличена, например до 2,45m, что приводит к образованию двухпарного контакта. Для конических передач с криволинейной формой зуба, в частности круговой, реализация двухпарного зацепления стандартным инструментом возможна только при малых углах наклона зубьев в пределах до 7°.
Дальнейшее повышение парности зацепления возможно в основном путем уменьшения угла профиля α и увеличения коэффициента высоты hα*, т. е. за счет высотно-профильной или только высотной модификации зубьев, когда hα* > 1,25m. В этих случаях для изготовления передач применяется специальный инструмент.
Синтез n-парных конических передач возможен при любых произвольных значениях n, что указывает на широкие возможности параметрической оптимизации передач по различным критериям качества. В таблицах 3 и 4, например, приведены значения коэффициентов εα для трехпарных передач с прямыми и круговыми зубьями при m = 1 без подреза и интерференции зубьев соответственно патентам РФ на полезные модели [3], [4]. В таблицах 5 и 6 — аналогичные данные по четырехпарным передачам [5], [6].

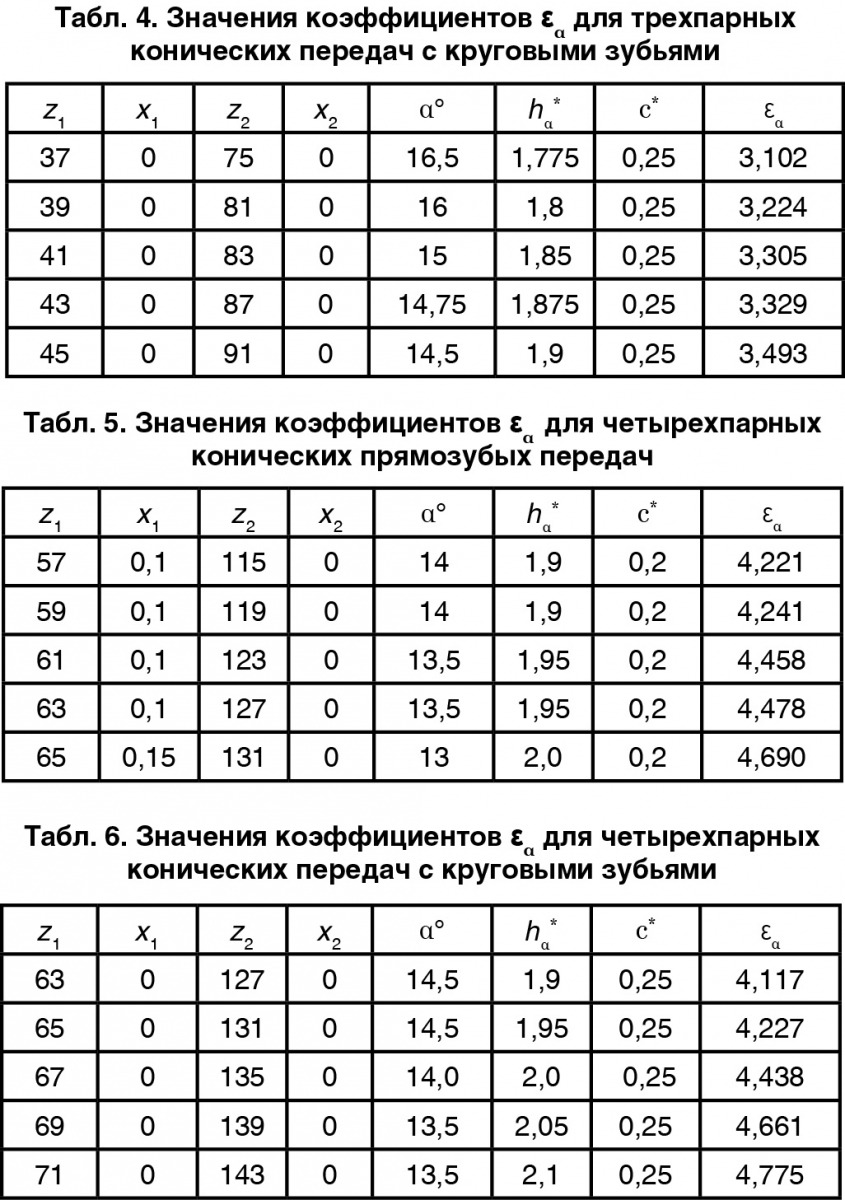
Как следует из таблиц (3)-(6) при приблизительно равных значениях чисел зубьев колес и соответствующих им параметров исходного контура значения коэффициентов εα для передач с прямыми и круговыми зубьями отличаются весьма незначительно. При этом по аналогии с цилиндрическими передачами [7] нагрузка на зубья при многопарном зацеплении уменьшается в зависимости от величины парности контакта. В первом приближении без учета жесткости и погрешностей изготовления прочностная выносливость многопарных передач по сравнению с аналогичными однопарными передачами увеличивается в среднем в n раз по изгибу и в √n раз по контакту. Это позволяет при близких значениях коэффициентов εα заменять передачи с круговым зубом на прямозубые, которые существенно менее трудоемки при изготовлении.
В результате за счет реализации многопарного зацепления можно значительно повысить несущую способность и прочность конических передач, а также во многих случаях преимущественно использовать прямозубые передачи как более технологичные. Например, нарезать зубья колес методом кругового протягивания, как наиболее производительным. При мелкосерийном или единичном производстве их традиционно можно нарезать модульными дисковыми или пальцевыми фрезами на горизонтально или вертикально-фрезерных станках.
В дополнение к этому при использовании прямозубых передач также существенно упрощается и конструкция подшипниковых опор. В виду того, что в этом случае осевая нагрузка на подшипники отсутствует, становится возможным вместо радиально-упорных подшипников устанавливать радиальные, которые и дешевле, и не требуют предварительного натяга. Такая замена существенно снижает общую трудоемкость изготовления и монтажа конических передач.
В итоге широкое применение многопарных конических передач в сочетании с возможной заменой передач с криволинейным зубом на прямозубые позволяет значительно повысить качество и эффективность передач.
Мельников Владимир Зиновьевич, к. т.н.
Московский государственный машиностроительный университет (МАМИ)
E-mail: melcapr@list.ru
Литература
1. ГОСТ 19624-74. Передачи зубчатые конические с прямыми зубьями. Расчет геометрии. М.: Изд-во стандартов, 1974. 26 с.
2. ГОСТ 19326-73. Передачи зубчатые конические с круговыми зубьями. Расчет геометрии. М.: Изд-во стандартов, 1974. 75 с.
3. Таратынов О. В., Мельников В. З., Болотина Е. М. Коническая прямозубая передача с трехпарным зацеплением. Патент РФ на полезную модель № 131110. Бюл.№ 22 от 10.08.2013.
4. Мельников В. З. Коническая передача с круговыми зубьями с трехпарным зацеплением. Патент РФ на полезную модель № 134265. Бюл. № 31 от 10.11.2013.
5. Мельников В. З., Таратынов О. В. Коническая прямозубая передача с четырехпарным зацеплением. Патент РФ на изобретение № 142182. Бюл. № 17 от 20.06.2014.
6. Мельников В. З. Коническая передача с круговыми зубьями с четырехпарным зацеплением. Патент РФ на полезную модель № 139974. Бюл. № 12 от 27.04.2014.
7. Мельников В. З. Синтез зубчатых передач с произвольным n-парным зацеплением. Вестник машиностроения. 2010. № 4, с. 29–31.