В данной работе ставиться проблема корректного замера деталей на координатно-измерительных машинах в случае плохо обусловленных базовых элементов. Рассматривается пример детали, контроль которой необходимо провести. Иллюстрируется способ коррекции базовой плоскости для последующего обмера детали на КИМ.

Возможности современного оборудования предполагают постоянное уменьшение производственных допусков на размеры деталей, и в настоящее время они гораздо меньше, чем были ранее. Одновременно с ужесточением допусков повышается доля трудоемкости операций контроля в технологическом процессе изготовления деталей и изделий. В машиностроении контроль занимает около 15% общей трудоемкости продукции, а в капитальных вложениях доля измерительных средств и контрольного оборудования достигает 20% объема инвестиций [1]. Поэтому точность измерений становится все более важным фактором в стремлении поддерживать и улучшать качество продукции. При этом новые высокоточные станки требуют высокоскоростных методов измерений и контроля геометрических параметров деталей, соответствующих скоростям обработки на станках с ЧПУ. В настоящее время одним из таких средств контроля служат координатно-­измерительные машины (КИМ) — риc. 1. В КИМ используется координатный метод измерения, сводящийся к последовательному нахождению координат ряда точек изделия и последовательному расчету размеров. Главное преимущество указанного метода в универсальности и возможности автоматизации процесса измерения. КИМ значительно упрощает метрологическую подготовку производства новых изделий, так как отпадает необходимость создания значительного количества средств специальной измерительной оснастки [1].

Рис. 1. Координатно-­измерительная машина Mitutoyo
 

В качестве рабочего инструмента КИМ, как правило, использует контактный датчик, которым происходит «ощупывание» детали, геометрические параметры которой нужно определить. Современные КИМ позволяют измерять размеры с точностью до 0,28 мкм [2]. При этом для удобства помимо декартовой системы координат можно использовать полярную и цилиндрическую систему координат.

Перед началом измерения необходимо выполнить процедуру привязки (базирования) детали в рабочем пространстве КИМ. В процессе базирования происходит ограничение 6 степеней свободы системы координат по базовым поверхностям, измеряемым на детали. От правильности выполнения базирования зависит не только результат измерения, но и отсутствие столкновений и ошибок при работе машины.

На базовые элементы проецируются все последующие измерения, поэтому ошибка при базировании закладывает ошибку практически в каждую оцениваемую характеристику. Для уменьшения погрешности проводят черновое и чистовое базирование. Черновое базирование выполняется для грубого выравнивания системы координат, чистовое — для точного выравнивания системы координат, поэтому элементы измеряются в ЧПУ-режиме с большим количеством точек.

Значительное воздействие на результат оценки допусков оказывает отношение длины базового элемента и расстояния оценки (длина оцениваемого элемента, включая расстояние между ними). На этапе оценки, когда элементы измерены, оцениваемый элемент проецируется на базовый. Из-за этого результат оценки несет в себе долю ошибки базирования (погрешность измерения базового элемента). Величина этой доли напрямую зависит от отношения длины базового элемента и расстояния оценки — рис. 2.

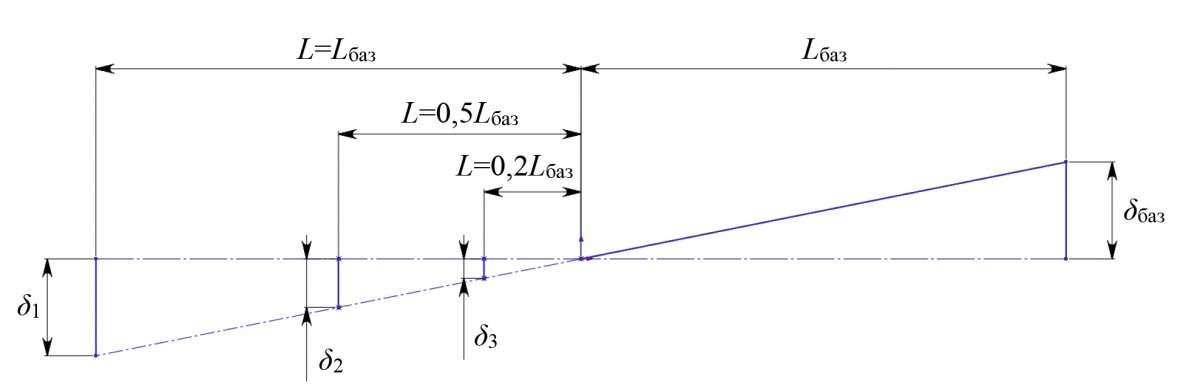
Рис. 2. Зависимость погрешности измерений от погрешности базирования
 

На рис. 2 δ₁, δ₂, δ₃— показаны ошибки измерения на расстоянии L, равном:
— длине базового элемента;
— половине базового элемента;
— одной пятой длины базового элемента.
δ_баз — ошибка базирования.

Например, при ошибке базирования в 3 мкм и длине базового элемента 10 мм, на длине 2 мм ошибка составит 0,6 мкм, на длине 5 мм — 1,5 мкм, на длине 10 мм — 3 мкм, а на длине 100 мм — 0,03 мм [3].

На практике при выборе базовых элементов стараются сделать так, чтобы их длина была не меньше длин оцениваемых элементов, но встречаются ситуации, когда данное правило выполнить не удается.

На рис. 3 показана матрица для изготовления детали кронштейн. Матрица имеет технологические отверстия и площадки для ее позиционирования. Необходимо оценить точность изготовления рабочей поверхности по электронной модели, допустимые предельные отклонения от электронной модели ±0,1 мм.

Рис. 3. Матрица для изготовления детали кронштейн
 

Базирование детали выполнено по следующим критериям:
— плоскость Оху набрана точками на площадках возле отверстий;
— начало координат (начало отсчета) — центр ближнего отверстия;
— направление оси Оу ориентированно по центру дальнего отверстия.

При сканировании поверхности по сечениям плоскостями, параллельными плоскости Oxz, сравнивая отсканированный контур с сечениями 3D-модели, видим отклонение фактического контура за пределы допуска — рис. 4. В данном случае отклонение вызвано не проблемой некачественного изготовления матрицы, а проблемой плохой обусловленности базовой плоскости Оху, поскольку в поперечном направлении область выбора точек на площадках возле отверстий в разы меньше области сканирования контура детали.

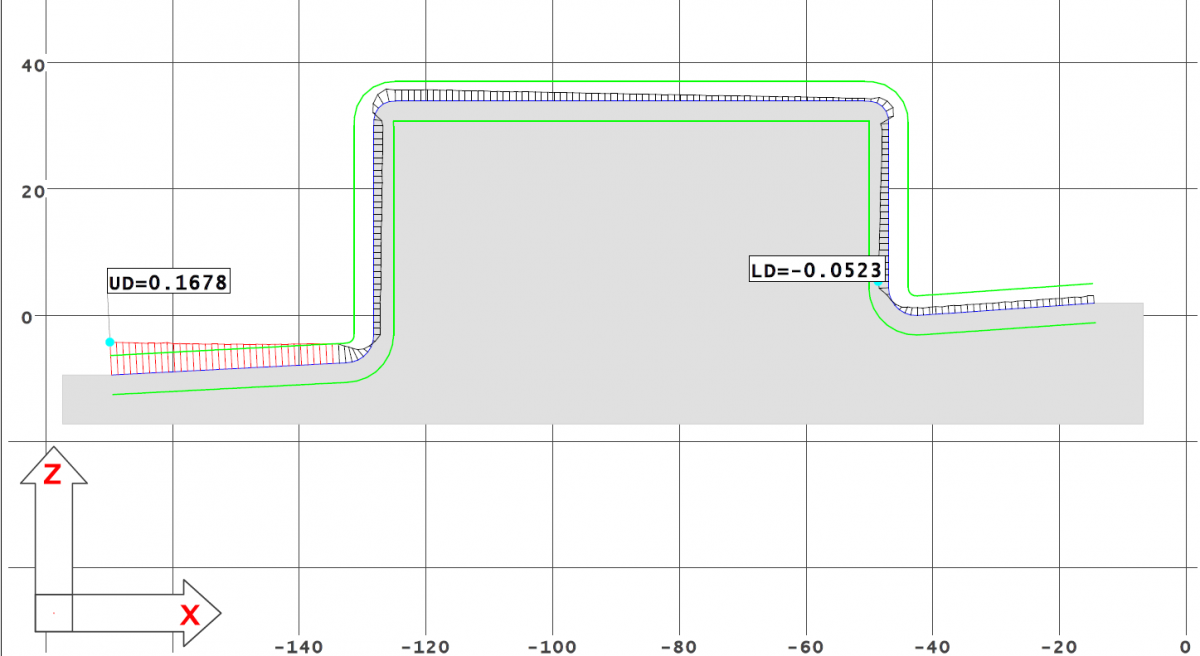
Рис. 4. Сравнение отсканированного контура с 3D-моделью

В математике существует метод решения так называемых некорректно поставленных задач. Основу метода заложил в начале 60‑х годов академик А.Н. Тихонов, дав ему название «метод регуляризации» [4].

Суть метода состоит в том, что постановка некорректной задачи дополняется некой априорной информацией количественного или качественного характера. В результате задача становиться корректной или условно корректной.

Плохо обусловленные задачи являются частным случаем некорректно поставленных задач, поэтому для них возможно применение метода регуляризации. Это открывает возможность правильной привязки деталей и, соответственно, возможность контроля на КИМ таких деталей, у которых базовые элементы привязки малы по отношению к измеряемым поверхностям.

Традиционно определение параметров математического объекта по результатам его измерений на КИМ осуществляется методом наименьших квадратов путем минимизации функции F(a), содержащей отклонения измеренных точек объекта:
    

 
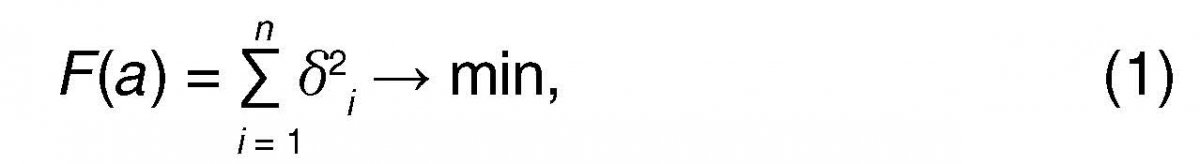
где  a = a₀,..,a_m — искомые параметры математического объекта; 
δ_i = │P'_i – P_i│,  i = 1, 2, ..., n  — отклонения измеренных точек; P_i = (x_i, y_i , z_i) — измеренная на объекте точка;
P'_i = (x'_i, y'_i, z_i') — точка на математическом объекте, соответствующая измеренной.

В плохо обусловленной задаче точка минимума функции F(a) нечетко выражена, функция в достаточно большой области имеет очень малый градиент. Программа минимизации при попадании в эту область перестает ощущать уменьшение функции и фиксирует минимум в случайной точке. В результате возникают большие ошибки в определении параметров математического объекта.

Улучшить обусловленность задачи можно за счет добавления априорной информации, которой могут быть номинальные значения параметров объектов. Как правило, измерения на КИМ выполняются с целью контроля, поэтому номинальные значения параметров известны, и именно их можно использовать для регуляризации задачи, добавив к функции (1) отклонения параметров от их номинальных значений:
       

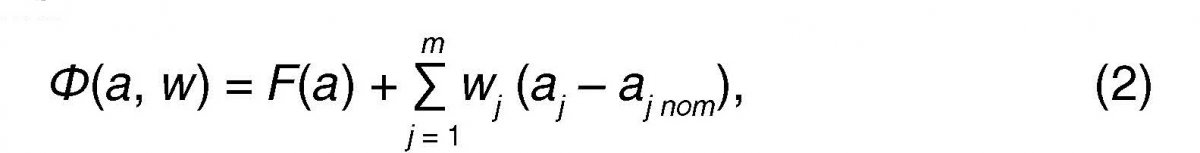
где w_j≥ 0,  j = 1, 2, ..., m — веса параметров (коэффициенты регуляризации); a_{j nom} — номинальное значение параметров.

В геометрическом контроле с помощью КИМ применяются два основных метода: традиционный метод, основанный на определении параметров геометрических объектов путем аппроксимации измеренных точек с помощью функции (1), и более поздний метод контроля по математической модели. Предлагаемый метод контроля, основанный на методе регуляризации, является обобщением двух существующих. Действительно, функция F(a) в (2) обеспечивает аппроксимацию точек измерений математическим объектом, а сумма квадратов отклонений параметров объекта от номинальных значений поддерживает его связь с идеальной моделью. Если положить w_j = 0,  j = 1, 2, ..., m, то минимизация функции (2) приведет к аппроксимации измеренных точек стандартным геометрическим объектом, то есть будет решена задача (1). При значениях весов w_j → ∞ влияние F(a) становится незначительным, что приводит к построению геометрического объекта с номинальными значениями параметров, относительно которого будут определены отклонения измеренных точек так же, как относительно математической модели.

Использование номинальных значений параметров для регуляризации измерительной задачи имеет и техническое обоснование. При изготовлении матрицы на производственном оборудовании ее параметры, такие как диаметры и координаты центров отверстий, были заложены в настройки станка, технологические приспособления, параметры инструмента, в управляющие программы для оборудования с ЧПУ и т. п. Поэтому имеются основания при построении математического объекта потребовать близости его параметров к их номинальным значениям, которые являлись обязывающими при изготовлении матрицы [5].

Для решения задачи контроля фактического контура изготовленной матрицы необходимо скорректировать базовую плоскость путем добавления ­какой-то априорной точки для последующего ее выравнивания, после чего произвести повторное сканирование сечения матрицы и сравнение полученного контура с сечениями 3D модели — рис. 5.

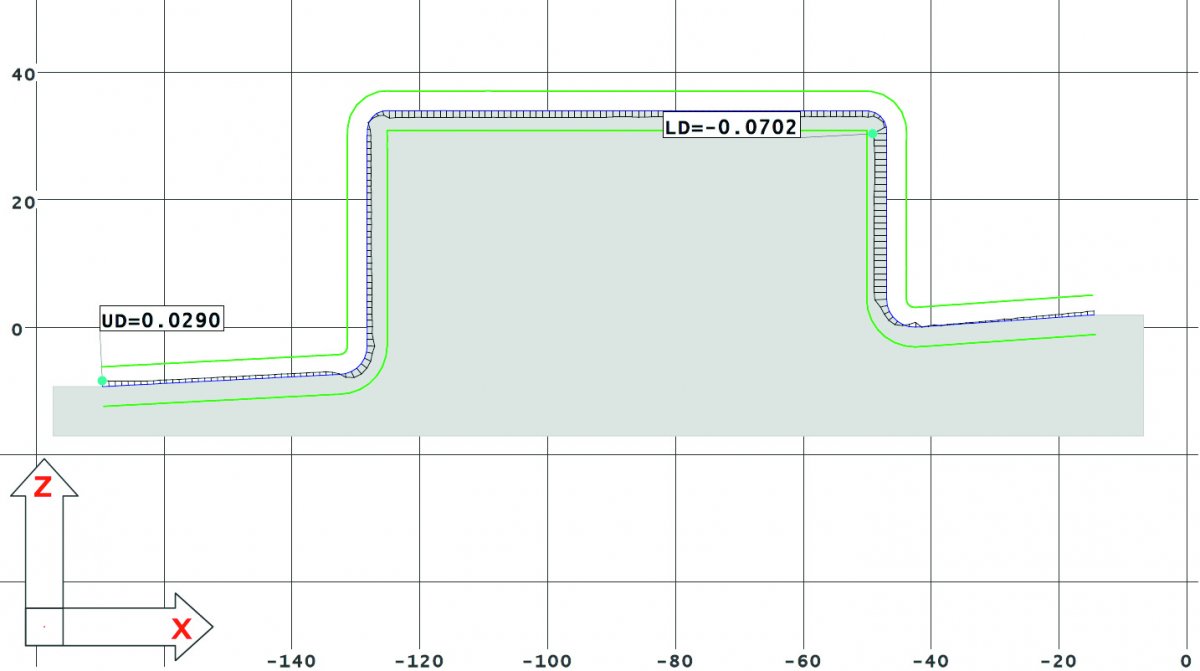
Рис. 5. Сравнение отсканированного контура после коррекции базовой плоскости с 3D-моделью

Как видно, фактический отсканированный контур целиком поместился в поле допуска. При этом отклонение от параллельности плоскостей, полученной по точкам площадок и откорректированной, составляет 0,0231 мм, что полностью укладывается в допуск на изготовление матрицы.

Литература

1. Координатные измерительные машины и их применение. Гапшис А. А., Каспарайтис А. Ю., Модестов М. Б. и др. М.: Машиностроение, 1988.  323 с., ил.
2. Сверхвысокоточные КИМ премиум-класса ООО «Митутойо РУС». https://shop.mitutoyo.ru/web/mitutoyo/ru_RU/mitutoyo/LEGEX%20Series%2032...КИМ%20премиум%20класса%20LEGEX/index.xhtml
3. Погрешности измерения и рекомендации по их устранению: Координатно-­измерительная машина (КИМ) / Михайлов Д.  — [б.м]: Издательские решения, 2020.  80 с. ISBN 987–5–4496–2013–2.
4. Тихонов А.Н. О решении некорректно поставленных задач и методе регуляризации // ДАН СССР. 1963. Т. 151. № 3. С. 501–504.
5. Суслин В. П. Джунковский А. В. Регуляризация плохо обусловленных задач в геометрических измерениях. // Известия МГТУ «МАМИ». 2009. № 2(8).

Источник журнал "РИТМ машиностроения" № 5-2022